2717 - 远足登山
题目描述
在一个风景如画的山区,有一位经验丰富的登山老师,名叫 L 老师。
L 老师带领着一群学生准备进行一次挑战性的登山远足。他们身处一个由 n 行 m 列的地图中,地图上标记了不同位置的海拔高度。
L 老师和学生们的起点是地图的最左上角,他们的目标是到达地图的最右下角。每个格子代表着一处不同的山地地形。
作为登山老师,L 老师希望为学生们规划一条耗费体力最小的路径,以确保他们能够安全、顺利地登上山顶。
路径的体力消耗是:路径上相邻格子之间的高度差的最大值。
现在的问题是,你需要帮助 L 老师计算他和学生们从起点到终点的最小体力消耗值,以帮助他们成功完成这次登山远足。
输入
n 表示格子的行数,m 表示格子的列数。
下面的 n \times m 个格子,表示消耗体力的参考值。
输出
从左上角走到右下角的最小体力消耗值。
样例
输入
3 3 1 2 2 3 8 2 5 3 5
输出
2
输入
3 3 1 2 3 3 8 4 5 3 5
输出
1
输入
5 5 1 2 1 1 1 1 2 1 2 1 1 2 1 2 1 1 2 1 2 1 1 1 1 2 1
输出
0
说明
【样例 1 解释】
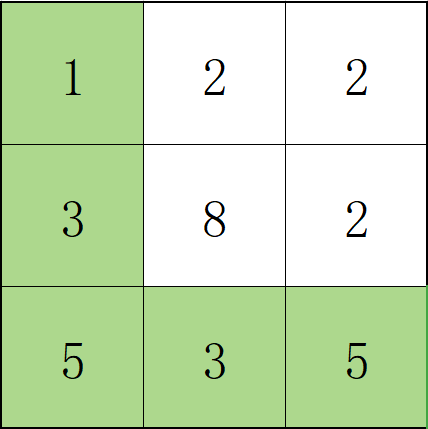
路径 1,3,5,3,5 连续格子的差值绝对值最大为 2 。
这条路径比路径 1,2,2,2,5 更优,因为另一条路径差值最大值为 3。
【样例 2 解释】
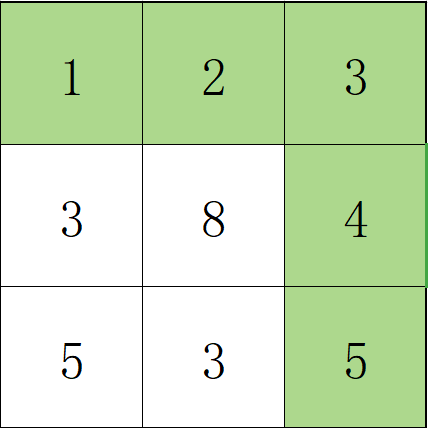
路径 1,2,3,4,5 的相邻格子差值绝对值最大为 1 ,比路径 1,3,5,3,5 更优。
【样例 3 解释】
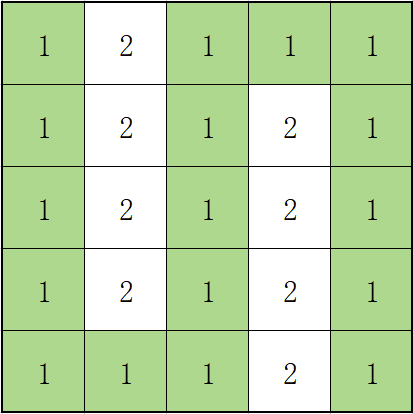
上图所示路径不需要消耗任何体力,故而输出 0。
【数据范围】
30\% 的数据满足:1 \le n \le 10 ,1 \le m \le 10,1 \le a[i][j] \le 10^2 。
60\% 的数据满足:1 \le n \le 10^2 ,1 \le m \le 10^2,1 \le a[i][j] \le 10^4 。
100\% 的数据满足:1 \le n \le 10^3 ,1 \le m \le 10^3,1 \le a[i][j] \le 10^6 。
标签