2963 - 直达航班
有 N 座城市(编号为 1 \sim N),城市之间有单向直达航班连接。直达航班的可用性通过 N 个长度为 N 的字符串 S_1, S_2, ..., S_N表示。
如果 S_i 的第 j 个字符为 Y,则表示从编号为 i 的城市到编号为 j 的城市有直达航班;如果为 N,则表示没有直达航班。
每座城市都销售一种纪念品;编号为 i 的城市销售价值为 A_i 的纪念品。
考虑以下问题:
小 T 目前位于城市 S,希望通过一些直达航班到达城市 T( T 与 S 不同)。每次他访问一个城市(包括 S 和 T ),他都会在那里购买一件纪念品。
如果从城市 S 到城市 T 存在多条路线,小 T 的决策规则如下:
1、尽量减少从城市 S 到城市 T 的经过直达航班数量。
2、尽量最大化他购买的纪念品的总价值。
判断他是否可以通过一个或多个直达航班,实现从城市 S 到城市 T 旅行。如果可以,找出满足上述条件的路线中,需要经过的"直达航班数量"和"纪念品总价值"。
给定 Q 对不同的城市(U_i, V_i)。对于每个 1 \le i \le Q,打印出当 S=U_i 且 T=V_i 时上述问题的答案。
第 1 行读入整数 N,代表城市的数量。
第 2 行读入 N 个整数 A_1 \sim A_N,代表编号为 1 \sim N 的城市,每个城市纪念品的价值。
接下来 N 行,读入 S_1 \sim S_N,代表直达航班的信息。
接下来读入整数 Q,代表询问的总数。
接下来 Q 行,每行读入两个整数 U_i,V_i,代表起止城市的编号。
打印 Q 行。
第 i 行(1 \le i \le Q)应包含以下内容:
如果他无法从城市 U_i 到城市 V_i 旅行,输出 Impossible。
如果可以,输出按照上述描述选择的路线中的"直达航班数量"和"纪念品总价值",以此顺序,用一个空格分隔。
输入
5 30 50 70 20 60 NYNYN NNYNN NNNYY YNYNY YNNNN 3 4 3 3 5 1 3
输出
1 90 1 130 2 150
输入
10 1 2 1 2 5 2 1 4 3 1 NYNNNYYNYN NNYNNNNNNN NNNYNNNNNN NNNNNNNNNN NNNYNNNNNN NNNNYNNNNN NNNNNNNYNN NNNYNNNNNN NNNNNNNNNY NNNYNNNNNN 3 1 4 4 1 1 10
输出
3 10 Impossible 2 5
样例 1 解释
样例 1 所对应的图,如下图所示。
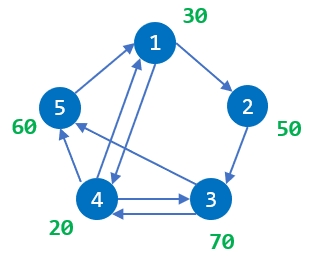
对于第 1 个询问,4 到 3 有 2 条不同的路线,但 4->3 直达的路线,经过航班最少,经过 1 个航班,购买到的纪念品总价值为 20+70=90。
对于第 2 个询问,3 到 5 有 2 条不同的路线,但 3->5 直达的路线,经过航班最少,经过 1 个航班,购买到的纪念品总价值为 70+60=130。
对于第 3 个询问,1 到 3 有 2 条不同的路线。
如果经过路线 1->2->3,经过 2 个航班,购买到的纪念品总价值为 30+50+70=150。
如果经过路线 1->4->3,经过 2 个航班,购买到的纪念品总价值为 30+20+70=120。
两条路线都经过了 2 个航班,但购买到的纪念品总价值最大为 150。
数据范围
对于 100\% 的数据,满足 2 \le N \le 300,1 \le A_i \le 10^9,S_i 是一个长度为 N 的字符串,由 Y 和 N 组成,1 \le Q \le N(N−1),1 \le U_i, V_i \le N,U_i \neq V_i。
东方博宜OJ