有 N 个点，编号为 1 \sim N，编号为 i 个点的值为 P_i。

有 M 条线段，编号为 1 \sim M，编号为 j 的线段，起止点的值为 S_j 和 T_j。

如果某个点恰好在一条线段的范围内，即满足：S_j \le P_i \le T_j，则我们认为该点可以管理该线段，该点和该线段成功形成了一个点线对。

现要求：每条线段最多可以选 1 个点来管理，编号为 j 的线段一旦选择了编号为 i 的点来管理，就不能选其他编号的点。

每个点最多只能管理 1 条线段。编号为 i 的点一旦负责管理了编号为 j 的线段，就不能选其他线段。

请编程计算出，最多能形成对少个点线对？

第 1 行读入整数 N,M 中间用空格隔开。

接下来 N 行，每行读入一个点的值。

再接下来 M 行，每行读入两个值，代表一条线段的起止点。

请注意：N 个点中，可能存在值相等的点，M 条线段中，可能存在起点相同、或者终点相同、或者起止点都相同的线段。

如果存在值相等的点，由于点的编号互不相同，认为是不同的点。同理，如果存在起止点相同的线段，由于他们的编号不同，也认为是不同的线段。

输出一个整数，代表形成点线对的最大数量。

样例 1 解释

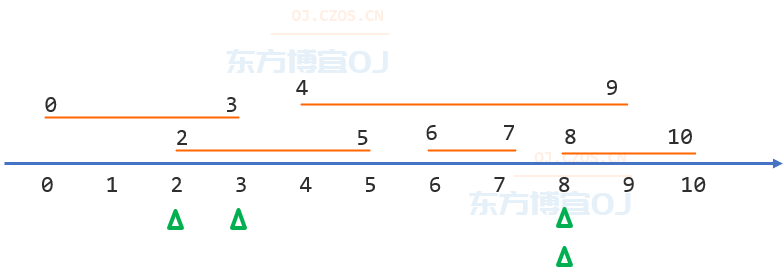
如下图所示，可以将点 2 和 线段 [0,3] 组成点线对，点 3 和 线段 [2,5] 组成点线对；有 2 个点 8，其中一个点 8 和线段 [4,9] 组成点线对，另一个点 8 和线段 [8,10] 组成点线对。

数据范围

对于 30\% 的数据，1 \le N,M \le 500。

对于 50\% 的数据，1 \le N,M \le 5000。

对于 100\% 的数据，1 \le N,M \le 20000，0 \le P_i \le 10^9，0 \le S_i \le T_i \le 10^9。

月赛贪心2023