某工厂中，每个工人生产的零件都需要经过严格的检验流程。

检验流程规定，每个工人生产的零件，必须经过 3 个不同的人检验合格之后，才能发放产品合格证书。

工厂共有 N 个工人，工人的工位之间通过双向的传送带连接（工位编号为 1 \sim N）。

位于 i 号工位的工人生产完一个零件之后，他会立刻通过传送带，直接传送给跟他相邻工位的工人进行检验。

相邻工位的工人检验完毕后，会在零件的检验标签上，标注检验结果，以及自己工位编号。然后，他会将该零件再次通过传送带，传送给相邻工位的工人进行检验。由于零件必须由 3 个不同的工人检验，因此他一定不会把零件传送给已经检验过该零件的工人。

需要注意的是，第 2 个工人检验结束后，可以将零件传送回 i 号工位的工人。即：由零件的生产者作为第 3 个检验人，也是允许的。

从编号为 i 的工位开始，零件检验会形成长度为 3 （经过了 3 条传送带）的检验路径。有意思的是，这样的路径可能不是唯一的。

比如，下图所示的工位分布图中，位于 1 号工位的工人生产的零件，可以有如下 7 条不同的合法检验路径。

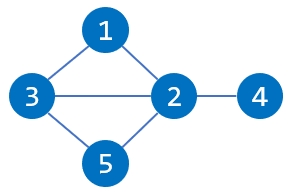
1 2 3 1
1 3 2 1
1 2 3 5
1 3 2 5
1 2 5 3
1 3 5 2
1 3 2 4

请编程计算出，如果每个工位都需要生产一个零件，并进行检验，所有的工位一共能形成多少条不同的合法检验路径。

第 1 行输入 2 个整数 N 和 M，分别表示工位数量和传送带数量。

接下来 M 行，每行输入两个整数 U_i 和 V_i，表示 U_i 号工位和 V_i 号工位之间存在一条传送带，任意两个工位之间最多只有一条传送带。

输出一个整数，表示所有工位一共能形成多少条不同的合法检验路径。

样例 1 解释

从每个点开始都有 2 条不同的检验路径，因此共有 6 条不同的检验路径。

样例 2 解释

本题的题目描述中的图，对应样例 2 的数据。

从 1 号点开始，存在 7 条检验路径。

从 2 号点开始，存在 6 条检验路径。

从 3 号点开始，存在 8 条检验路径。

从 4 号点开始，存在 4 条检验路径。

从 5 号点开始，存在 7 条检验路径。

因此，共有 32 条不同的合法检验路径。

数据范围

对于 30\% 的测评数据，满足 1 \le N \le 100，1 \le M \le 1000。

对于 80\% 的测评数据，满足 1 \le N \le 100，1 \le M \le 5000。

对于 100\% 的测评数据，满足 1 \le N \le 1000，1 \le M \le 10000，1 \le U_i,V_i \le N，U_i \neq V_i。

测试数据保证答案不超过 3 \times 10^7。

图论月赛2024