在一个深山中，人们为了喝到纯净的山泉水，每天都要往返于村庄和深山中的水源之间。

村长决定为村里修建一个大的蓄水池，将山泉水引入到水池中，解决村民生活用水的问题。建造水池的工程师，在调研了蓄水池选址区域的地质后发现，这里的地址差别比较大，在不同的位置能建造的蓄水池，能够建造的高度有差异。

比如，下图标注了 10 个等间隔的位置，任意两个相邻的位置间隔均为 1 个单位长度，在不同位置建造蓄水池的高度。

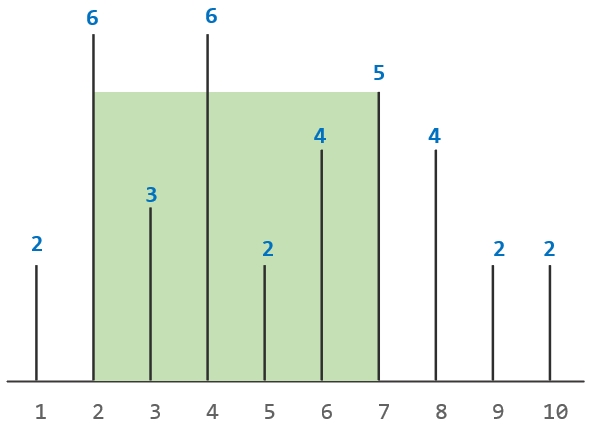
现要求选定 2 个不同的位置，作为蓄水池的起点和终点，建造水池，要求建造出的水池在最大储水量的情况下横截面积最大。

如果选择在第 2 个位置和第 8 个位置建造水池，那么水池实际储水高度为 min(6,4)=4 个单位长度，水池的宽度为 8-2=6 个单位长度，因此水池最大储水量的横截面的面积为 6 \times 4 = 24。

而如果选择在第 2 个位置和第 7 个位置建造水池，那么水池的实际储水高度为 min(6,5)=5 个单位长度，水池的宽度为 7-2=5 个单位长度，因此水池最大储水量的横截面的面积为 5 \times 5 = 25。

经过计算可知，上述例子中，水池最大储水量的横截面的面积为 25。

现给出 N 个等间隔的，任意两个相邻位置的间隔均为 1 个单位长度，并给出在每个位置建造水池的高度，请编程计算出，水池中最大储水量的横截面积。

第一行包含一个整数 N，表示有 N 个可以作为蓄水池起止点的备选位置。

第二行包含 N 个整数，第 i 个整数 A_i 表示在第 i 个点建造水池的高度。

输出一个整数，表示最大储水量的横截面积。

数据范围

对于 30\% 的数据，满足 2 \leq N \leq 20, 1 \leq A_i \leq 50。

对于 50\% 的数据，满足 2 \leq N \leq 500, 1 \leq A_i \leq 1000。

对于 70\% 的数据，满足 2 \leq N \leq 5000, 1 \leq A_i \leq 1000。

对于 100\% 的数据，满足 2 \leq N \leq 1,000,000, 1 \leq A_i \leq 1,000,000,000。

线段树月赛2024