2734 - 最佳路线
小 A 计划暑假开车从家出发,到某著名旅游城市旅行。
从小 A 的家所在的城市到目标城市,共需经过 N 个城市和 M 条不同的单向高速公路。N 个城市编号为 1 \sim N,小 A 的家在编号为 1 的城市,他想要去的城市编号为 N。
出发前,他安装了最新款的导航,该导航不仅可以计算出,从任意编号为 X (X \in [1,N])的城市去编号为 N 的城市,路程之和最短的路线。还可以计算出从编号为 X 的城市去编号为 N 的城市,拥挤度总和最小的路线。
小 A 是一个节俭的人,他希望尽量的走路程总和最短的路线,这样可以节约油费。同时,他也是一个非常不喜欢拥堵的人,他又希望,规划好的路线是拥挤度总和最小的路线。鱼与熊掌,很难兼得。
于是,聪明的小 A 想出了一个极好的规划路线的方法。从 1 号城市出发,假设他当前行驶在一条从 U 号城市去 V 号城市的单向高速路上,如果这条高速路不在从 U 号城市到 N 号城市的最短路的路线上,他的不高兴度就会增加 1。同样的,如果这条高速路不在从 U 号城市去 N 号城市的拥挤度之和最小的路线上,他的不高兴度也会增加 1。也就是说,当小 A 行驶在某条高速路上时,他的不高兴度可能不增加,也可能增加 1 或者增加 2。
请你编程帮助小 A 规划一条路线,使得他从 1 号城市到 N 号城市,不高兴度的和最小,你只需要输出这个最小的不高兴度的和。
第 1 行输入两个整数 N,M,中间用空格隔开。
接下来 M 行,每行输入 4 个整数,U_i,V_i,L_i,C_i,代表一条高速公路从编号为 U_i 的城市连通到编号为 V_i 的城市,该高速路的长度为 L_i,拥挤度为 C_i。
请注意:U_i 和 V_i 的值可能相等。
输出小 A 从 1 号城市行驶到 N 号城市,不高兴度和的最小值。
输入
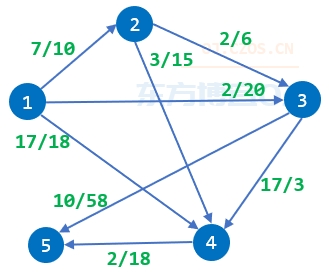
5 8 1 2 7 10 3 5 10 58 4 5 2 18 2 4 3 15 3 4 17 3 1 3 2 20 1 4 17 18 2 3 2 6
输出
1
输入
11 20 1 3 2 6 3 5 2 6 5 7 2 6 7 9 2 6 9 11 2 12 1 2 6 3 2 4 6 3 4 6 6 3 6 8 6 3 8 11 12 2 1 10 5 5 2 1 3 2 3 1 3 2 4 10 3 2 5 10 3 2 6 10 3 2 7 10 3 2 8 10 3 2 9 10 3 2 10 1 3 2
输出
3
样例 1 解释
从 1 号城市出发:
沿 1 -> 4 单向高速路去 4 号城市,该高速路不在 1 号城市到 5 号城市最短路的路线上,因此不高兴度增加 1 。但该高速路在 1 号城市到 5 号城市拥挤度之和最小的路线上。
接下来沿 4 -> 5 单向高速路去 5 号城市,该高速路既在 4 号城市到 5 号城市最短路的路线上,又在 4 号城市到 5 号城市拥挤度之和最小的路线上,因此不高兴度不增加。
数据范围
对于 30\% 的数据,2 \le N \le 10,1 \le M \le 20。
对于 100\% 的数据,2 \le N \le 10^4,1 \le M \le 5 \times 10^4,1 \le U_i,V_i \le N,1 \le L_i,C_i \le 10^5。
测试数据确保,一定存在路线可以让小 A 从 1 号城市出发,顺利到达 N 号城市。