2714 - 特种小队
某次演习,我军 A 特种作战小队深入敌后,在完成任务后开始撤退。
为帮助 A 小队撤退,军团侦查兵连夜侦察了小队附近的敌军小队布防情况,并电告 A 小队。
小队队长收到电报后,打开作战地图,标注了我小队当前位置、小队需要到达的接应点的位置,以及每个敌军小队的所在地区的坐标。
作战地图是一个二维平面图,我小队当前在 S_1,S_2 处,需尽快到达位于 0,0 点的接应点。敌军有 N 个小队在附近布防,第 i 个敌军小队目前在 X_i,Y_i 处布防。
我小队在该二维平面中可以从某坐标,移动到上下左右四方向的相邻点的坐标,移动次数和移动位置没有限制。因弹药有限,队长决定尽可能避免移动到有敌军小队的位置,如果不得不移动到有敌军小队的位置,我小队必须快速消灭该点的敌军小队,继续前进。
假设小队有足够的能力消灭撤退路径中遇到的每个敌军小队,且敌军小队的布防在我小队撤退过程中不会发生变化。
请编程求解出,我小队至少要消灭几个敌军小队,才能达到接应点的位置。
第 1 行输入整数 N,S_1,S_2,数字之间用空格隔开。
接下来 N 行,每行读入两个整数 X_i,Y_i。
测试数据确保我小队的当前位置、我小队需要到达的接应点都不会有敌小队布防,也不存在任意两个敌小队在同一个位置布防的情况。
输出一个整数,代表我小队最少要消灭的敌军小队的数量。
输入
7 6 3 6 2 5 2 4 3 7 3 5 4 6 4 1 1
输出
1
输入
12 5 6 5 8 4 7 5 7 6 7 3 6 4 6 6 6 7 6 4 5 5 5 6 5 5 4
输出
2
输入
6 6 3 6 2 4 3 7 3 5 4 6 4 1 1
输出
0
样例 1 解释
样例 1 所示的作战地图如下:
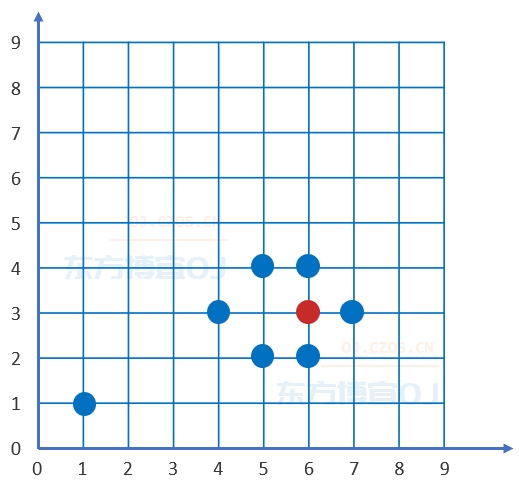
位于 6,3 位置的我小队只需要消灭除了 1,1 位置以外的其他 6 个敌小队中的一个,就可以顺利到达位于 0,0 位置的接应点。
数据范围
对于 20\% 的数据,满足 1 \le N \le 20,1 \le S_1,S_2 \le 20,1 \le X_i,Y_i \le 20。
对于 100\% 的数据,满足 1 \le N \le 5 \times 10^4,1 \le S_1,S_2 \le 1000,1 \le X_i,Y_i \le 1000。